Integral formulations of volumetric transmittance

Iliyan Georgiev*
Autodesk
Zackary Misso*
Dartmouth College
Toshiya Hachisuka
The University of Tokyo

Derek Nowrouzezahrai
McGill University
Jaroslav Křivánek
Charles University, Prague
Chaos Czech a. s. Wojciech Jarosz
Dartmouth College

* Authors with equal contribution.

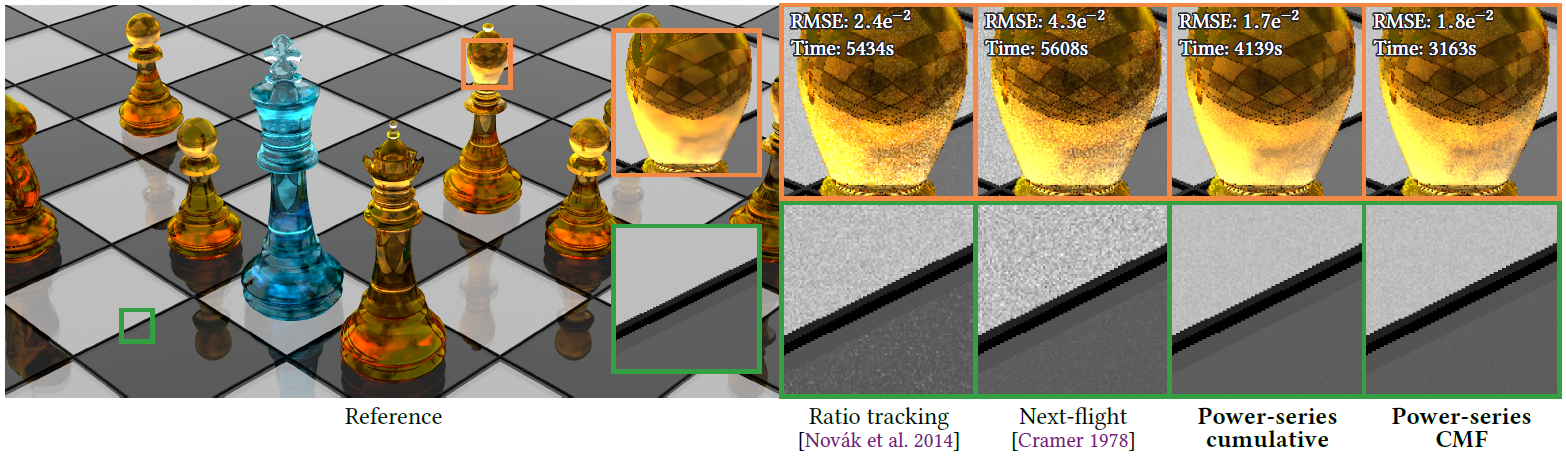Equal-lookup comparisons of various estimators in a scene with both homogeneous (chess board) and heterogeneous (chess pieces) media. Our proposed estimators (in bold) trade more extinction lookups for lower-variance estimates of transmittance. RMSE and render times are for the entire image.

Abstract

Computing the light attenuation between two given points is an essential yet expensive task in volumetric light transport simulation. Existing unbiased transmittance estimators are all based on “null-scattering” random walks enabled by augmenting the media with fictitious matter. This formulation prevents the use of traditional Monte Carlo estimator variance analysis, thus the efficiency of such methods is understood from a mostly empirical perspective. In this paper, we present several novel integral formulations of volumetric transmittance in which existing estimators arise as direct Monte Carlo estimators. Breaking from physical intuition, we show that the null-scattering concept is not strictly required for unbiased transmittance estimation, but is a form of control variates for effectively reducing variance. Our formulations bring new insight into the problem and the efficiency of existing estimators. They also provide a framework for devising new types of transmittance estimators with distinct and complementary performance tradeoffs, as well as a clear recipe for applying sample stratification.

Reference

Iliyan Georgiev, Zackary Misso, Toshiya Hachisuka, Derek Nowrouzezahrai, Jaroslav Křivánek, and Wojciech Jarosz. Integral formulations of volumetric transmittance. ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia 2019), 38(6), 2019.
DOI | BibTeX

Links and Downloads

paper fulltext	supplemental web page	code

pdf (11 MB)	external link	GitHub

Acknowledgments

All images have been rendered using PBRT [Pharr et al. 2016]. The chessboard and pieces in Figs. 1 and 8 are from TurboSquid. The cloud model in Fig. 9 is from Disney Research. The Fox model in Fig. 11 is from Thingiverse.

This work was supported by a gift from Autodesk, National Science Foundation Grant IIS-1812796, Czech Science Foundation Grant 19-07626S, and Charles University Grant SVV-2017-260452.