Abstract
Monte Carlo techniques for light transport simulation rely on importance sampling when constructing light transport paths.
Previous work has shown that suitable sampling distributions can be recovered from particles distributed in the scene prior to rendering.
We propose to represent the distributions by a parametric mixture model trained in an on-line (i.e. progressive) manner from a potentially infinite stream of particles.
This enables recovering good sampling distributions in scenes with complex lighting, where the necessary number of particles may exceed available memory.
Using these distributions for sampling scattering directions and light emission significantly improves the performance
of state-of-the-art light transport simulation algorithms when dealing with complex lighting.
Downloads
| Paper: | Supplemental document: | Supplemental images: | BibTeX: | Source code: | Documentation: |
 |
 |
 |
 |
 |
 |
| (.pdf) | (.pdf) | (.pdf) | (.bib) | (.zip) | (.pdf) |
Images
Video
BibTeX
@article{Vorba:2014:OnlineLearningPMMinLTS,
author = {Ji\v{r}\'i Vorba and Ond\v{r}ej Karl\'ik and Martin \v{S}ik and
Tobias Ritschel and Jaroslav K\v{r}iv\'{a}nek},
title = {On-line Learning of Parametric Mixture Models for Light Transport Simulation},
journal = {ACM Transactions on Graphics (Proceedings of SIGGRAPH 2014)},
volume = {33},
number = {4},
year = {2014},
month = {aug},
keywords = {light transport simulation, importance sampling, parametric density estimation, on-line expectation maximization}
}
Acknowledgements
The work was supported by Charles University in Prague, project GA UK No 580612,
by the grant SVV–2014–260103, and by the Czech Science Foundation
P202-13-26189S.
We thank Jan Beneš, Alexander Wilkie, and Iliyan Georgiev for their feedback on the paper
draft and to Ludvík Koutný for providing us with the Living Room scene.
We have used these two renderers:
Jiří Vorba © 2014
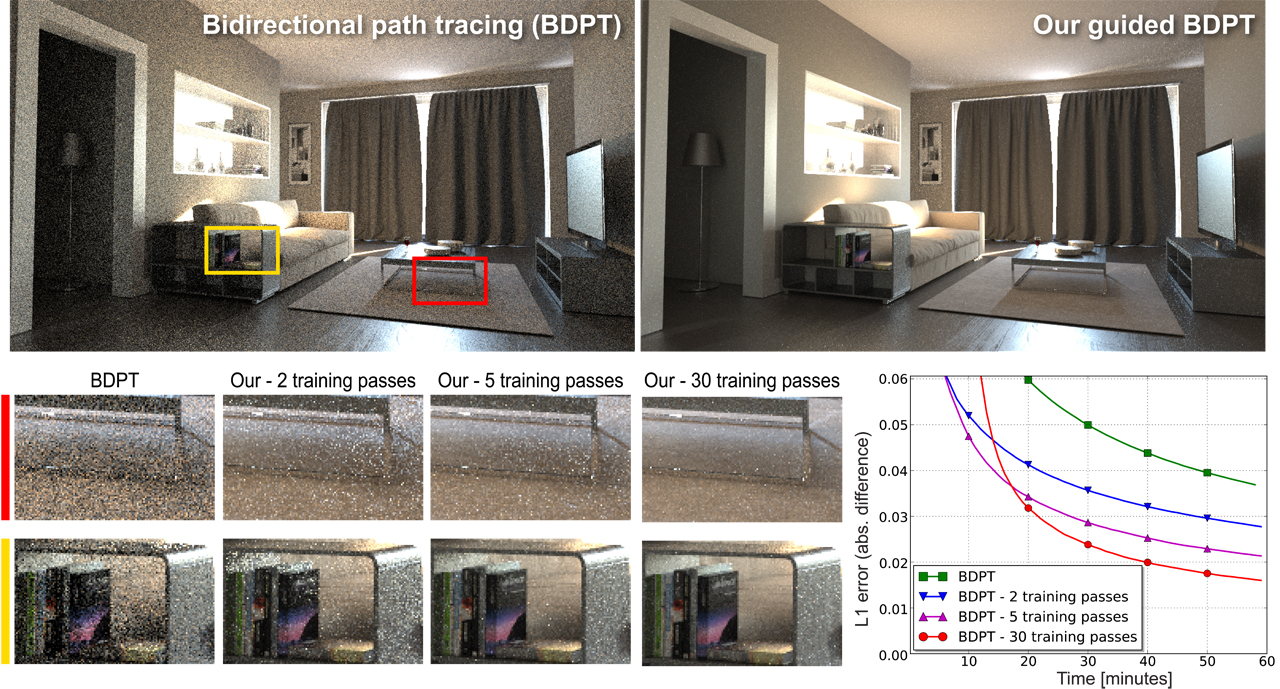 We render a scene featuring difficult visibility with bidirectional path tracing (BDPT) guided by
our parametric distributions learned on-line in a number of training passes (TP).
The insets show equal-time (1h) comparisons of images obtained with different numbers of training passes.
Time spent on training is included in the total rendering time.
The results reveal that the time spent on additional training passes is quickly amortized by the superior
performance of the subsequent guided rendering.
We render a scene featuring difficult visibility with bidirectional path tracing (BDPT) guided by
our parametric distributions learned on-line in a number of training passes (TP).
The insets show equal-time (1h) comparisons of images obtained with different numbers of training passes.
Time spent on training is included in the total rendering time.
The results reveal that the time spent on additional training passes is quickly amortized by the superior
performance of the subsequent guided rendering.


